
FREEMAT DIAGONAL OF MATRIX GENERATOR
Singularity in the remaining integral along the generator of the panel and for these problems this work is applicable. However, for the particular class of axisymmetric 3D problems, the first azimuthal integration over the panel results again in a logarithmic There have been a number of papers addressing the problem of integrating functions like this for general 3D problems in the BEM, both numerically and analytically, although this is outside the scope of this paper. The distance between the observation point and the point on the panel). Much of the aforementioned story is the same for three-dimensional problems, except that, in this case, the bounding surface is represented by a mesh, made up

However, some panels are close to the observation point, and the corresponding integral are regular, but are also strongly-varying, and some researchers also apply special treatment to these nearly-singular integrals. All of the other integrals are regular and are therefore amenable to standard quadrature methods, often Gauss-Legendre quadrature rules for their optimal efficiency. For constant elements, where the functional representation of boundary properties is a constant value on each panel, the diagonal components of the matrices correspond to singular integrals. For two-dimensional problems, the logarithmic singularity occurs when the observation point lies on the panel over which the integration is applied. In the boundary element method, the integrals are generally found numerically, although in a number of special cases the integrals can by evaluated analytically. By applying a suitable integral equation method, such as collocation, the boundary integral equation is resolved into a linear system of equations, with each row of the matrices representing a geometrical line integral of each panel with respect to a particular boundary observation (e.g. The boundary is represented by a set of panels, with functional representations of the properties on those panels that ascribe the boundary elements. The governing partial differential equation is reformulated as a boundary integral equation, and the latter is solved in order to determine unknown boundary properties. Integrals like the one above typically occur in implementation of the two-dimensional (2D) boundary element method (BEM), when the observation point lies at the parametric mid-point of the element or panel. In the outcome, it is noted that the method proposed method may be generalised and applied to stronger singularities. In this work, we look at finding near-optimal quadrature rules for the numerical evaluation of this class of integral. A weak logarithmic singularity is one in which the behaviour near the singularity is of the form

Is a continuously differentiable function, except for having weak logarithmic singularity at its mid-point (when
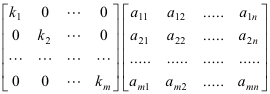
FREEMAT DIAGONAL OF MATRIX WINDOWS
I'm on Windows 7, so your path may be different.In this paper the problem of determining an efficient quadrature rule for and integral of the form This tells FreeMat to override the internal functions for tril and triu and use the m-files. Then, I added the path for the FREEMAT directory (c:\Program Files (x86)\FreeMat) to the path using the path tool (Menu: Tools->Path Tool). I created the files tril.m and triu.m in the FREEMAT directory (c:\Program Files(x86)\FreeMat) as follows:Ī(i,:) = I looked at this and was successful at overriding the built in functions with new functions that reflect the MATLAB behavior.


 0 kommentar(er)
0 kommentar(er)
